i will implement linear regression which can be adapted classification easily, i use Matlab by following the Dr. Andrew Ng's class. You can watch the classes online from here.
While implementing i also came across a very nice blog post, actually only dataset differs, in this case i use the original dataset given by the Dr. Ng, more details of the code below can be reached from here (DSPlog )
download data

and the batch gradient descent update rule is

theta_vec = [0 0]'; alpha = 0.007; err = [0 0]'; for kk = 1:1500 h_theta = (x*theta_vec); h_theta_v = h_theta*ones(1,n); y_v = y*ones(1,n); theta_vec = theta_vec - alpha*1/m*sum((h_theta_v - y_v).*x).'; err(:,kk) = 1/m*sum((h_theta_v - y_v).*x).'; end
Cost Function:
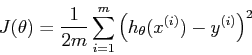
For different values of theta, in this case theta0 and theta1, we can plot the cost function J(theta) in 3d space or as a contour.
j_theta = zeros(250, 250); % initialize j_theta theta0_vals = linspace(-5000, 5000, 250); theta1_vals = linspace(-200, 200, 250); for i = 1:length(theta0_vals) for j = 1:length(theta1_vals) theta_val_vec = [theta0_vals(i) theta1_vals(j)]'; h_theta = (x*theta_val_vec); j_theta(i,j) = 1/(2*m)*sum((h_theta - y).^2); end end figure; surf(theta0_vals, theta1_vals,10*log10(j_theta.')); xlabel('theta_0'); ylabel('theta_1');zlabel('10*log10(Jtheta)'); title('Cost function J(theta)'); figure; contour(theta0_vals,theta1_vals,10*log10(j_theta.')) xlabel('theta_0'); ylabel('theta_1') title('Cost function J(theta)');
%linear regression using gradient descent algorithm to find the coefficients, %there are many ways to find the coefficients but now we apply gradient descent %one dimensional data, with an output x = load('ex2x.dat'); y = load('ex2y.dat'); figure % open a new figure window plot(x, y, 'o'); ylabel('Height in meters') xlabel('Age in years') m = length(y); % store the number of training examples x = [ones(m, 1), x]; % Add a column of ones to x n = size(x,2); %this part is for minimizing the Theta_vec: coefficients. theta_vec = [0 0]'; alpha = 0.007; err = [0 0]'; for kk = 1:10000 h_theta = (x*theta_vec); h_theta_v = h_theta*ones(1,n); y_v = y*ones(1,n); theta_vec = theta_vec - alpha*1/m*sum((h_theta_v - y_v).*x).'; err(:,kk) = 1/m*sum((h_theta_v - y_v).*x)'; end figure; plot(x(:,2),y,'bs-'); hold on plot(x(:,2),x*theta_vec,'rp-'); legend('measured', 'predicted'); grid on; xlabel('x'); ylabel('y'); title('Measured and predicted '); j_theta = zeros(250, 250); % initialize j_theta theta0_vals = linspace(-5000, 5000, 250); theta1_vals = linspace(-200, 200, 250); for i = 1:length(theta0_vals) for j = 1:length(theta1_vals) theta_val_vec = [theta0_vals(i) theta1_vals(j)]'; h_theta = (x*theta_val_vec); j_theta(i,j) = 1/(2*m)*sum((h_theta - y).^2); end end figure; surf(theta0_vals, theta1_vals,10*log10(j_theta.')); xlabel('theta_0'); ylabel('theta_1');zlabel('10*log10(Jtheta)'); title('Cost function J(theta)'); figure; contour(theta0_vals,theta1_vals,10*log10(j_theta.')) xlabel('theta_0'); ylabel('theta_1') title('Cost function J(theta)');



good
ReplyDelete